DIGITAL MODULATION ; DIGITAL MODULATION TYPES AND RELATIVE EFFICIENCIES

3. Digital modulation types and relative efficiencies

This section covers the main digital modulation formats, their main applications, relative spectral efficiencies and some variations of the main modulation types as used in practical systems. Fortunately, there are a
limited number of modulation types which form the building blocks of any system.
3.1 Applications
This table covers the applications for different modulation formats in both wireless communications and video.

Modulation	format Application
MSK, GMSK	GSM, CDPD
BPSK	Deep space telemetry, cable modems
QPSK, ¹/4 DQPSK	Satellite, CDMA, NADC, TETRA, PHS, PDC, LMDS, DVB-S, cable (return path), cable modems, TFTS
OQPSK	CDMA, satellite
FSK, GFSK	DECT, paging, RAM mobile data, AMPS, CT2, ERMES, land mobile, public safety
8, 16 VSB	North American digital TV (ATV), broadcast, cable
8PSK	Satellite, aircraft, telemetry pilots for monitoring broadband video systems
16 QAM	Microwave digital radio, modems, DVB-C, DVB-T
32 QAM	Terrestrial microwave, DVB-T
64 QAM	DVB-C, modems, broadband set top boxes, MMDS
256 QAM	Modems, DVB-C (Europe), Digital Video (US)

Although this note focuses on wireless communications, video applications have also been included in the table for completeness and because of their similarity to other wireless communications.

3.1.1 Bit rate and symbol rate

To understand and compare different modulation format efficiencies, it is important to first understand the difference between bit rate and symbol rate. The signal bandwidth for the communications channel needed depends on the symbol rate, not on the bit rate.

Symbol rate = bit rate / the number of bits transmitted with each symbol

Bit rate is the frequency of a system bit stream. Take, for example, a radio with an 8 bit sampler, sampling at 10 kHz for voice. The bit rate, the basic bit stream rate in the radio, would be eight bits multiplied by 10K samples per second, or 80 Kbits per second. (For the moment we will ignore the extra bits required for synchronization, error correction, etc.).

Figure 10. Bit Rate and Symbol Rate

Figure 10 is an example of a state diagram of a Quadrature Phase Shift Keying (QPSK) signal. The states can be mapped to zeros and ones. This is a common mapping, but it is not the only one. Any mapping can be used. 

The symbol rate is the bit rate divided by the number of bits that can be transmitted with each symbol. If one bit is transmitted per symbol, as with BPSK, then the symbol rate would be the same as the bit rate of 80 Kbits per second. If two bits are transmitted per symbol, as in QPSK, then the symbol rate would be half of the bit rate or 40 Kbits per second. Symbol rate is sometimes called baud rate. Note that baud rate is not the same as bit rate. These terms are often confused. If more bits can be sent with each symbol, then the same amount of data can be sent in a narrower spectrum.

This is why modulation formats that are more complex and use a higher number of states can send the same information over a narrower piece of the RF spectrum.

3.1.2 Spectrum (bandwidth) requirements

An example of how symbol rate influences spectrum requirements can be seen in eight-state Phase Shift Keying (8PSK). It is a variation of PSK.

There are eight possible states that the signal can transition to at any time. The phase of the signal can take any of eight values at any symbol time. Since 23 = 8, there are three bits per symbol. This means the symbol

rate is one third of the bit rate. This is relatively easy to decode.

Figure 11. Spectrum Requirements

3.1.3 Symbol clock

The symbol clock represents the frequency and exact timing of the transmission of the individual symbols. At the symbol clock transitions, the transmitted carrier is at the correct I/Q (or magnitude/phase) value to

represent a specific symbol (a specific point in the constellation).

3.2 Phase Shift Keying

One of the simplest forms of digital modulation is binary or Bi-Phase Shift Keying (BPSK). One application where this is used is for deep space telemetry. The phase of a constant amplitude carrier signal moves between zero and 180 degrees. On an I and Q diagram, the I state has two different values. There are two possible locations in the state diagram, so a binary one or zero can be sent. The symbol rate is one bit per symbol.

Figure 12. Phase Shift Keying

A more common type of phase modulation is Quadrature Phase Shift Keying (QPSK). It is used extensively in applications including CDMA (Code Division Multiple Access) cellular service, wireless local loop, Iridium (a voice/data satellite system) and DVB-S (Digital Video Broadcasting - Satellite). Quadrature means that the signal shifts between phase states which are separated by 90 degrees. The signal shifts in increments of 90 degrees from 45 to 135, –45, or –135 degrees. These points are chosen as they can be easily implemented using an I/Q modulator. Only two I values and two Q values are needed and this gives two bits per symbol. There are four states because 22 = 4. It is therefore a more bandwidth-efficient type

of modulation than BPSK, potentially twice as efficient.

3.3 Frequency Shift Keying

Frequency modulation and phase modulation are closely related. A static frequency shift of +1 Hz means that the phase is constantly advancing at the rate of 360 degrees per second (2 ¹ rad/sec), relative to the phase of the unshifted signal.

Figure 13. Frequency Shift Keying

FSK (Frequency Shift Keying) is used in many applications including cordless and paging systems. Some of the cordless systems include DECT (Digital Enhanced Cordless Telephone) and CT2 (Cordless Telephone 2). In FSK, the frequency of the carrier is changed as a function of the modulating signal (data) being transmitted. Amplitude remains unchanged. In binary FSK (BFSK or 2FSK), a “1” is represented by one frequency and a “0” is represented by another frequency.

3.4 Minimum Shift Keying

Since a frequency shift produces an advancing or retarding phase, frequency shifts can be detected by sampling phase at each symbol period. Phase shifts of (2N + 1) ¹/2 radians are easily detected with an I/Q demodulator.

At even numbered symbols, the polarity of the I channel conveys the transmitted data, while at odd numbered symbols the polarity of the Q channel conveys the data. This orthogonality between I and Q simplifies detection algorithms and hence reduces power consumption in a mobile receiver. The minimum frequency shift which yields orthogonality of I and Q is that which results in a phase shift of ± ¹/2 radians per symbol (90 degrees per symbol). FSK with this deviation is called MSK (Minimum Shift Keying). The deviation must be accurate in order to generate repeatable 90 degree phase shifts. MSK is used in the GSM (Global System for Mobile Communications) cellular standard. A phase shift of +90 degrees represents a data bit equal to “1”, while –90 degrees represents a “0”. The peak-to-peak frequency shift of an MSK signal is equal to one-half of the bit rate.

FSK and MSK produce constant envelope carrier signals, which have no amplitude variations. This is a desirable characteristic for improving the power efficiency of transmitters. Amplitude variations can exercise

nonlinearities in an amplifier’s amplitude-transfer function, generating spectral regrowth, a component of adjacent channel power. Therefore, more efficient amplifiers (which tend to be less linear) can be used with

constant-envelope signals, reducing power consumption.

MSK has a narrower spectrum than wider deviation forms of FSK. The width of the spectrum is also influenced by the waveforms causing the frequency shift. If those waveforms have fast transitions or a high slew rate, then the spectrum of the transmitter will be broad. In practice, the waveforms are filtered with a Gaussian filter, resulting in a narrow spectrum. In addition, the Gaussian filter has no time-domain overshoot,

which would broaden the spectrum by increasing the peak deviation. 

MSK with a Gaussian filter is termed GMSK (Gaussian MSK).

3.5 Quadrature Amplitude Modulation

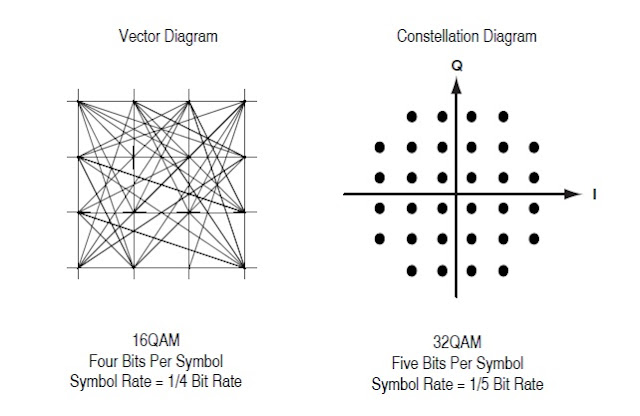
Another member of the digital modulation family is Quadrature Amplitude Modulation (QAM). QAM is used in applications including microwave digital radio, DVB-C (Digital Video Broadcasting - Cable) and modems.

Figure 14. Quadrature Amplitude Modulation

In 16-state Quadrature Amplitude Modulation (16QAM), there are four I values and four Q values. This results in a total of 16 possible states for the signal. It can transition from any state to any other state at every symbol time. Since 16 = 24, four bits per symbol can be sent. This consists of two bits for I and two bits for Q. The symbol rate is one fourth of the bit rate.

So this modulation format produces a more spectrally efficient transmission. It is more efficient than BPSK, QPSK or 8PSK. Note that QPSK is the same as 4QAM.

Another variation is 32QAM. In this case there are six I values and six Q values resulting in a total of 36 possible states (6x6=36). This is too many states for a power of two (the closest power of two is 32). So the four corner symbol states, which take the most power to transmit, are omitted. This reduces the amount of peak power the transmitter has to generate. Since 25 = 32, there are five bits per symbol and the symbol rate is one fifth of the bit rate.

The current practical limits are approximately 256QAM, though work is underway to extend the limits to 512 or 1024 QAM. A 256QAM system uses 16 I-values and 16 Q-values giving 256 possible states. Since 28 = 256, each symbol can represent eight bits. A 256QAM signal that can send eight bits per symbol is very spectrally efficient. However, the symbols are very close together and are thus more subject to errors due to noise and distortion. Such a signal may have to be transmitted with extra power (to effectively spread the symbols out more) and this reduces power efficiency as compared to simpler schemes. 

Compare the bandwidth efficiency when using 256QAM versus BPSK modulation in the radio example in section 3.1.1 (which uses an eight-bit sampler sampling at 10 kHz for voice). BPSK uses 80 Ksymbols-per-second sending 1 bit per symbol. A system using 256QAM sends eight bits per symbol so the symbol rate would be 10 Ksymbols per second. A 256QAM system enables the same amount of information to be sent as BPSK using only one eighth of the bandwidth. It is eight times more bandwidth efficient. However, there is a tradeoff. The radio becomes more complex and is more susceptible to errors caused by noise and distortion. Error rates of higher-order QAM systems such as this degrade more rapidly than QPSK as noise or interference is introduced. A measure of this degradation would be a higher Bit Error Rate (BER).

In any digital modulation system, if the input signal is distorted or severely attenuated the receiver will eventually lose symbol lock completely. If the receiver can no longer recover the symbol clock, it cannot demodulate the signal or recover any information. With less degradation, the symbol clock can be recovered, but it is noisy, and the symbol locations themselves are noisy. In some cases, a symbol will fall far enough away from its intended position that it will cross over to an adjacent position. The I and Q level detectors used in the demodulator would misinterpret such a symbol as being in the wrong location, causing bit errors. QPSK is not as efficient, but the states are much farther apart and the system can tolerate a lot more noise before suffering symbol errors. QPSK has no intermediate states between the four corner-symbol locations so there is less opportunity for the demodulator to misinterpret symbols. QPSK requires less transmitter power than QAM to achieve the same bit error rate.

3.6 Theoretical bandwidth efficiency limits

Bandwidth efficiency describes how efficiently the allocated bandwidth is utilized or the ability of a modulation scheme to accommodate data, within a limited bandwidth. This table shows the theoretical bandwidth efficiency limits for the main modulation types. Note that these figures cannot actually be achieved in practical radios since they require perfect modulators, demodulators, filter and transmission paths.

Modulation format	Theoretical bandwidth efficiency limits
MSK	1 bit/second/Hz
BPSK	1 bit/second/Hz
QPSK	2 bits/second/Hz
8PSK	3 bits/second/Hz
16 QAM	4 bits/second/Hz
32 QAM	5 bits/second/Hz
64 QAM	6 bits/second/Hz
256 QAM	8 bits/second/Hz

If the radio had a perfect (rectangular in the frequency domain) filter, then the occupied bandwidth could be made equal to the symbol rate.

Techniques for maximizing spectral efficiency include the following:

• Relate the data rate to the frequency shift (as in GSM).

• Use premodulation filtering to reduce the occupied bandwidth. Raised cosine filters, as used in NADC, PDC, and PHS give the best spectral efficiency.

• Restrict the types of transitions.

3.7 Spectral efficiency examples in practical radios

The following examples indicate spectral efficiencies that are achieved in some practical radio systems.

The TDMA version of the North American Digital Cellular (NADC) system, achieves a 48 Kbits-per-second data rate over a 30 kHz bandwidth or 1.6 bits per second per Hz. It is a ¹/4 DQPSK based system and transmits two bits per symbol. The theoretical efficiency would be two bits per second per Hz and in practice it is 1.6 bits per second per Hz.

Another example is a microwave digital radio using 16QAM. This kind of signal is more susceptible to noise and distortion than something simpler such as QPSK. This type of signal is usually sent over a direct line-of-sight microwave link or over a wire where there is very little noise and interference. In this microwave-digital-radio example the bit rate is 140 Mbits per second over a very wide bandwidth of 52.5 MHz. The spectral efficiency is 2.7 bits per second per Hz. To implement this, it takes a very clear line-of-sight transmission path and a precise and optimized high-power transceiver.

Digital modulation types - variations

The modulation types outlined in sections 3.2 to 3.4 form the building blocks

for many systems. There are three main variations on these basic building

blocks that are used in communications systems: I/Q offset modulation,

differential modulation, and constant envelope modulation.

3.8 I/Q offset modulation

The first variation is offset modulation. One example of this is Offset QPSK (OQPSK). This is used in the cellular CDMA (Code Division Multiple Access) system for the reverse (mobile to base) link.

Figure 15. I-Q “Offset” Modulation

In QPSK, the I and Q bit streams are switched at the same time. The symbol clocks, or the I and Q digital signal clocks, are synchronized. In Offset QPSK (OQPSK), the I and Q bit streams are offset in their relative alignment by one bit period (one half of a symbol period). This is shown in the diagram. Since the transitions of I and Q are offset, at any given time only one of the two bit streams can change values. This creates a dramatically different constellation, even though there are still just two I/Q values. This has power efficiency advantages. In OQPSK the signal trajectories are modified by the symbol clock offset so that the carrier amplitude does not go through or near zero (the center of the constellation).

The spectral efficiency is the same with two I states and two Q states. The reduced amplitude variations (perhaps 3 dB for OQPSK, versus 30 to 40 dB for QPSK) allow a more power-efficient, less linear RF power amplifier to be used.

3.9 Differential modulation

The second variation is differential modulation as used in differentialvQPSK (DQPSK) and differential 16QAM (D16QAM). Differential means that the information is not carried by the absolute state, it is carried by the transition between states. In some cases there are also restrictions on allowable transitions. This occurs in ¹/4 DQPSK where the carrier trajectory does not go through the origin. A DQPSK transmission system can transition from any symbol position to any other symbol position.

The ¹/4 DQPSK modulation format is widely used in many applications including

• cellular

  -NADC- IS-54 (North American digital cellular)

  -PDC (Pacific Digital Cellular)

• cordless

   -PHS (personal handyphone system)

• trunked radio

  -TETRA (Trans European Trunked Radio)

The ¹/4 DQPSK modulation format uses two QPSK constellations offset by 45 degrees (¹/4 radians). Transitions must occur from one constellation to the other. This guarantees that there is always a change in phase at each symbol, making clock recovery easier. The data is encoded in the magnitude and direction of the phase shift, not in the absolute position on the constellation. One advantage of ¹/4 DQPSK is that the signal trajectory does not pass through the origin, thus simplifying transmitter design. Another is that ¹/4 DQPSK, with root raised cosine filtering, has better spectral efficiency than GMSK, the other common cellular modulation type.

Figure 16. “Differential” Modulation

3.10 Constant amplitude modulation

The third variation is constant-envelope modulation. GSM uses a variation of constant amplitude modulation format called 0.3 GMSK (Gaussian Minimum Shift Keying).

Figure 17. Constant Amplitude Modulation

In constant-envelope modulation the amplitude of the carrier is constant, regardless of the variation in the modulating signal. It is a power-efficient scheme that allows efficient class-C amplifiers to be used without

introducing degradation in the spectral occupancy of the transmitted signal. However, constant-envelope modulation techniques occupy a larger bandwidth than schemes which are linear. In linear schemes, the amplitude of the transmitted signal varies with the modulating digital signal as in BPSK or QPSK. In systems where bandwidth efficiency is more important than power efficiency, constant envelope modulation is not as well suited.

MSK (covered in section 3.4) is a special type of FSK where the peak-to-peak frequency deviation is equal to half the bit rate.

GMSK is a derivative of MSK where the bandwidth required is further reduced by passing the modulating waveform through a Gaussian filter.

The Gaussian filter minimizes the instantaneous frequency variations over time. GMSK is a spectrally efficient modulation scheme and is particularly useful in mobile radio systems. It has a constant envelope, spectral

efficiency, good BER performance and is self-synchronizing.

Effects of going through the origin

Take, for example, a QPSK signal where the normalized value changes from 1, 1 to –1, –1. When changing simultaneously from I and Q values of +1 to I and Q values of –1, the signal trajectory goes through the origin (the I/Q value of 0,0).

The origin represents 0 carrier magnitude. A value of 0 magnitude indicates that the carrier amplitude is 0 for a moment.

Not all transitions in QPSK result in a trajectory that goes through the origin.

If I changes value but Q does not (or vice-versa) the carrier amplitude changes a little, but it does not go

through zero. Therefore some symbol transitions will result in a small amplitude variation, while others will result in a very large amplitude variation. The clock-recovery circuit in the receiver must deal with this amplitude variation uncertainty if it uses amplitude variations to align the receiver clock with the transmitter clock.

Spectral regrowth does not automatically result from these trajectories that pass through or near the origin. If the amplifier and associated circuits are perfectly linear, the spectrum (spectral occupancy or occupied bandwidth) will be unchanged.

The problem lies in nonlinearities in the circuits.

A signal which changes amplitude over a very large range will exercise these nonlinearities to the fullest extent. These nonlinearities will cause distortion products. In continuously-modulated systems they will cause “spectral regrowth” or wider modulation sidebands (a phenomenon related to intermodulation distortion). Another term which is sometimes used in this context is “spectral splatter”. However this is a term that is more correctly used in association with the increase in the bandwidth of a signal caused by pulsing on and off.

Lihat juga

DIGITAL MODULATION; INTRODUCTION
DIGITAL MODULATION ; WHY DIGITAL MODULATION
DIGITAL MODULATION ; USING I/Q MODULATION TO CONVEY INFORMATION 
DIGITAL MODULATION ; DIGITAL MODULATION TYPES AND RELATIVE EFFICIENCIES 
DIGITAL MODULATION ; FILTERING 
DIGITAL MODULATION ; DIFFERENT WAYS OF LOOKING AT A DIGITAL MODULATED SIGNAL TIME AND FREQUENCT DOMAIN VIEW 
DIGITAL MODULATION ; SHARING THE CHANNEL 
DIGITAL MODULATION ; HOW DIGITAL TRANSMITTER AND RECEIVER WORK 
DIGITAL MODULATION ; MEASUREMENT ON DIGITAL RF COMMINICATION SYSTEMS 
DIGITAL MODULATION ; SUMMARY 
DIGITAL MODULATION ; OVERVIEW OF COMMUNICATION SYSTEM 
DIGITAL MODULATION ; GLOSSARY OF TERM