ANEKA INFO TEKNIK: TUTORIAL SALURAN TRANSMISI ; KECEPATAN PERAMBATAN GELOMBANG

Jika tegangan awal diterapkan pada ujung saluran pengiriman , tegangan yang sama kemudian akan muncul beberapa jauh dari ujung saluran pengiriman. Hal ini berlaku untuk setiap perubahan tegangan, apakah perubahan itu melompat dari nol menjadi nilai tertentu atau penurunan dari tertentu nilai menuju ke nol. Perubahan tegangan akan dilakukan sepanjang saluran dengan laju yang konstan.
Ingat bahwa induktansi dari saluran akan menunda pengisian kapasitansi saluran. Kecepatan perambatan tersebut berhubungan dengan nilai-nilai L dan C. Jika induktansi dan kapasitansi dari saluran rf diketahui, waktu yang dibutuhkan untuk setiap gelombang untuk berjalan di sepanjang saluran dapat ditentukan. Untuk melihat bagaimana ini bekerja amati hubungan berikut:

Q = IT

Rumus ini menunjukkan bahwa total muatan atau kuantitas sama dengan arus dikalikan dengan waktu arus mengalir. juga:

Q = CE

Rumus ini menunjukkan bahwa total muatan pada kapasitor adalah sama dengan kapasitansi dikalikan dengan tegangan kapasitor.
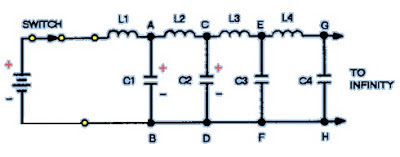
Jika saklar pada gambar di bawah ditutup untuk waktu tertentu, muatan (Q) listrik meninggalkan baterai dapat dihitung dengan menggunakan persamaan Q = IT. Listrik meninggalkan baterai dan masuk ke saluran, dan aka mengisi kapasitor. Besarnya pengisian ini dihitung dengan menggunakan persamaan Q = CE.

Gambar Dc diterapkan pada ekivalen saluran transmisi

Karena tidak ada muatan yang hilang, jumlah total muatan yang meninggalkan meninggalkan baterai selama T adalah sama dengan muatan total muatan pada saluran. Oleh karena itu:

Q = IT = CE

Karena setiap kapasitor mengakumulasi muatan sama dengan CE, tegangan di setiap induktor harus berubah. Karena C1 pada gambar diatas mengisi tegangan E, titik A naik ke potensial E volt sedangkan titik B masih di nol volt. Hal ini membuat E muncul di L2. Saat C2 mengisi, titik B naik ke potensi E volt seperti halnya titik A. Pada saat ini, titik B berada pada E volt dan titik C naik. Dengan demikian, kita memiliki aksi terus menerus dari tegangan yang bergerak di sepanjang saluran yang tak terbatas.
Dalam sebuah induktor, komponen rangkaian ini saling terkait, seperti yang ditunjukkan dalam rumus

Hal ini menunjukkan bahwa tegangan induktor berbanding lurus dengan induktansi dan perubahan arus, tapi berbanding terbalik dengan perubahan waktu. Karena arus dan waktu mulai dari nol, perubahan waktu (DT) dan perubahan arus (DI) yang sama dengan waktu akhir (T) dan arus akhir (I). Untuk kasus ini persamaan menjadi:

ET = LI

Jika tegangan E diterapkan untuk waktu (T) di induktor (L), arus akhir (I) akan mengalir. Persamaan berikut menunjukkan bagaimana tiga istilah (T, L, dan C) terkait:

IT = CE

ET = LI

Untuk memudahkan, Anda dapat menemukan T dalam hal L dan C dengan cara berikut. Kalikan anggota kiri dan kanan masing-masing persamaan sebagai berikut:

(IT).(ET) = (CE).(LI)

Keemudian

EIT² = LCEI

Dibagi dengan

(EI) : T² = LC

Dan

T = Ö(LC)

Persamaan akhir ini digunakan untuk mencari waktu yang dibutuhkan oleh perubahan tegangan untuk berjalan dalam satuan panjang, karena L dan C diberikan dalam hal satuan panjang. Kecepatan gelombang dapat ditemukan oleh:

V = D / T or D / Ö(LC)

Dimana: D adalah unit fisik panjang
Ini adalah tingkat di mana gelombang berjalan dalam satuan panjang. Unit L dan C adalah henrys dan Farad. T dalam detik per satuan panjang dan V adalah dalam unit panjang per detik.

LIHAT JUGA

PENGANTAR

TERMINOLOGY

Macam-macam Transmision line

Two wire/paralel line/Kabel sejajar
Twisted Pair

Shielded Pair

Coaxial Lines

Rigid & flexible coaxial

Waveguide

Losses pada Saluran transmisi

Panjang Saluran Transmisi
Teori Saluran Transmisi
Konstanta Lumped dan konstanta distribusi

Medan Elektromagnetik sekitar saluran Transmisi